在NLP实验室混了有一段时间,模型多少也算跑过几个,但是一直把它当黑箱用,没有动力去研究其内部构造。这两天终于抽出精力把大名鼎鼎的《Attention is all you need》看完了,想趁着兴趣还在,把矩阵在整个模型中的流动给系统性描述一遍。
本文包括:
- 矩阵每一层的形状变化情况
- Pytorch代码实现
那就开始吧。要记住模型的目的是输入序列,输出序列
先验知识——PyTorch自定义层和块
pytorch里面一切自定义操作基本上都是继承nn.Module类来实现的,包括整个Model和某一层的Layer。
Transformer结构总览
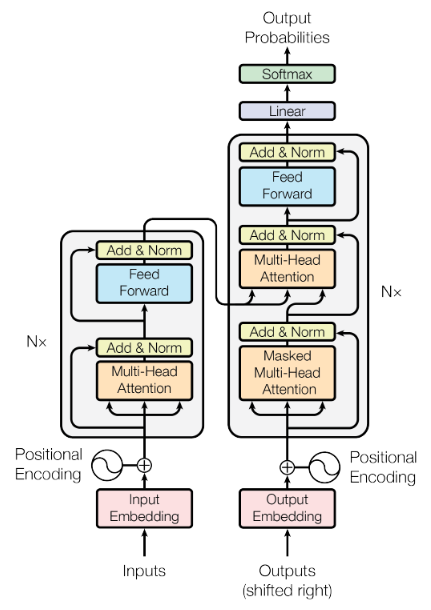
怎么理解呢?首先要认识到一点,Transformer是一个双输入无监督模型。以中译英翻译任务为例,我们试图把句子“我爱中国”翻译成”I love China”,那么Inputs作为输入1,获取的是中文“我爱中国”的id列表;标准答案应为“I love China
具体地,模型分为几个部分。
- 前处理:我们先输入一个Tensor作为Inputs,形状往往是$(batch_size,max_seq_len)$,此时第一维是经典的batch_size维,第二维往往是把一句话的所有单词一一映射到id上去所形成的id_list,接着我们通过Embedding层升维度为$(batch_size,max_seq_len,embedding_len)$。Embedding的思路见如何训练一个词向量,但这不是本文的重点,因为我们直接使用Embedding层就可以了。然后,我们定义了某个神奇的公式,构造出一个和Embedding形状完全一样的三维输出,加到它上面去。这个公式的神奇之处就在于他可以把字的相对位置信息赋予Embedding向量,实验表明这对模型的效果提升是大有帮助的。
- Encoder层:Encoder层是一个复杂的子层连叠六次的产物,这里我们称每一个子层为子Encoder层。具体怎么操作呢?先不管,当成黑箱用就好了。
- Decoder层:Decoder层是一个复杂的子层连叠六次的产物,这里我们称每一个子层为子Decoder层。同理,当成黑箱就好。
- 线性层+Softmax:改变形状,得到输出。
数据准备
先是一些固定的参数,我们写在外面。
1
2
3
4
5
6
#Embedding维度512,编码解码各叠6层,每一头矩阵64维,8头注意力,FF层变成2048维,这些都是论文定死的方案
d_model = 512
n_layers = 6
n_heads = 8
d_q = d_k = d_v = 64
d_ff = 2048
使用Dataset+Dataloader对象构建数据集合,这样的好处是PyTorch自带大量的API,可以帮助你做各种处理。不过在这个小批量的例子中可能没有什么感觉。我们构建了两条数据,都是双输入+单输出形式的。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
# S: 开始符号
# E: 结束符号
# P: 补齐位,如句子长度不一,可用若干个P补到最长的那个句子。
sentences = [
# enc_input dec_input dec_output
['ich mochte ein bier P', 'S i want a beer .', 'i want a beer . E'],
['ich mochte ein cola P', 'S i want a coke .', 'i want a coke . E']
]
# Padding Should be Zero
src_vocab = {'P' : 0, 'ich' : 1, 'mochte' : 2, 'ein' : 3, 'bier' : 4, 'cola' : 5}
src_vocab_size = len(src_vocab)
tgt_vocab = {'P' : 0, 'i' : 1, 'want' : 2, 'a' : 3, 'beer' : 4, 'coke' : 5, 'S' : 6, 'E' : 7, '.' : 8}
idx2word = {i: w for i, w in enumerate(tgt_vocab)}
tgt_vocab_size = len(tgt_vocab)
src_len = 5 # enc_input max sequence length
tgt_len = 6 # dec_input(=dec_output) max sequence length
def make_data(sentences):
enc_inputs, dec_inputs, dec_outputs = [], [], []
for i in range(len(sentences)):
enc_input = [[src_vocab[n] for n in sentences[i][0].split()]] # [[1, 2, 3, 4, 0], [1, 2, 3, 5, 0]]
dec_input = [[tgt_vocab[n] for n in sentences[i][1].split()]] # [[6, 1, 2, 3, 4, 8], [6, 1, 2, 3, 5, 8]]
dec_output = [[tgt_vocab[n] for n in sentences[i][2].split()]] # [[1, 2, 3, 4, 8, 7], [1, 2, 3, 5, 8, 7]]
enc_inputs.extend(enc_input)
dec_inputs.extend(dec_input)
dec_outputs.extend(dec_output)
return T.LongTensor(enc_inputs), T.LongTensor(dec_inputs), T.LongTensor(dec_outputs)
enc_inputs, dec_inputs, dec_outputs = make_data(sentences)
class MyDataSet(Data.Dataset):
def __init__(self, enc_inputs, dec_inputs, dec_outputs):
super().__init__()
self.enc_inputs = enc_inputs
self.dec_inputs = dec_inputs
self.dec_outputs = dec_outputs
def __len__(self):#必须重写__len__()方法
return self.enc_inputs.shape[0]
def __getitem__(self, idx):#必须重写__getitem__()方法,模仿即可
return self.enc_inputs[idx], self.dec_inputs[idx], self.dec_outputs[idx]
loader = Data.DataLoader(MyDataSet(enc_inputs, dec_inputs, dec_outputs), batch_size=2, shuffle=False)
预编码部分
Inputs:我们不考虑batch_size这一维度,即我们只考虑一个句子被输入模型的情况。可以理解为一个一维的id_列表。如输入“我爱你”,那么人工定义字典{“我”:0,”爱”:1,”你”:2}后,真实输入为[[0,1,2]]。此时形状为$(None,max_seq_len)$。
Input Embedding:1维升2维,论文中的$d_{model}=512$。在Transformer中Embedding矩阵怎么获得并不重要,只需要知道两点:其一,Transformer本身就可以用来做Embedding训练任务;其二,也可用训练好的Embedding层做别的任务,如经典的机器翻译。此时形状为$(None,sen_len,d_model)$。
Positional Encoding: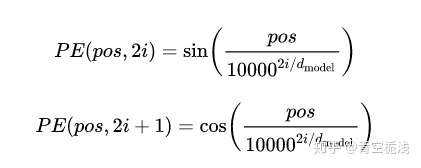
其中pos是位置,i是维度。如爱的pos=1,那么就要通过上述的公式建立出PE(1,1-512)的值。此时形状为$(None,max_seq_len,d_model)$。
相加:把Embedding Vector和Positional Encoding相加,此时的输出已经包含词的内容信息和位置信息。此时形状为$(None,max_seq_len,d_model)$,可以把它输入到Encoder层中了,不妨取名叫作enc_inputs。
我们注意到,Positional Encoding其实和输入的句子具体内容没什么关系,充其量和
1
2
3
4
5
6
7
8
9
def PositionalEncoding(position, d_model):
positional_embedding = T.zeros((position,d_model))
for i in range(position):
for j in range(d_model):
if j%2 == 0:
positional_embedding[i,j] = np.sin(i/np.power(10000,j/d_model))
else:
positional_embedding[i,j] = np.cos(i/np.power(10000,(j-1)/d_model))
return T.FloatTensor(positional_embedding)
Encoder
从预编码部分拿到$(None,max_seq_len,d_model)$形状的矩阵,要做这样一些事情。
1. Multi-Head Attention 2. add&norm 3. FNN 4. add&norm 5. 然后把它打包重复接六次即可。Multi-Head Attention
首先,我们要使用enc_inputs同时生成三个矩阵,分别是查询矩阵Q,键矩阵K,值矩阵V。生成方式很简单,用模型学一个线性层就行,而生成的形状只要把Embedding的最后一维长度512压缩到64即可。因为我们这里要做一个8头操作,所以通过压缩维度的方式可以保证参数数量不增加。这三个矩阵的形状都是$(None,max_seq_len,64)$。
接着,我们用Q和trans(K)点乘,容易注意到得到的乘积形状是$(None,max_seq_len,max_seq_len)$,这里可以理解成我们在试图计算词语词的某种相似度得分,比如$(None,i,j)$描述的是这句话中第i词和第j词的“相似度”,准确地说是“Attention”,即我们在研究某句话的第j词时,要花多少注意在第i词上。
然后用mask矩阵遮挡一些词的信息,如图所示。这一步的目的是让预测序列的时候最多只能获得之前字的信息。在论文里,Encoder层不需要mask,可以传全1矩阵,但Decoder矩阵要用下半全1,上半全零的矩阵mask掉。
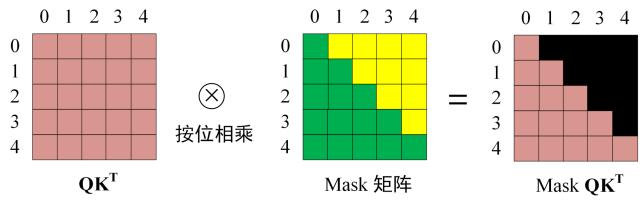
随后过softmax,形状仍为,$(None,i,j)$刻画了i对j的注意力标准化得分,且在0-1之间,行求和为1。
最后和V相乘,得到输出Z。
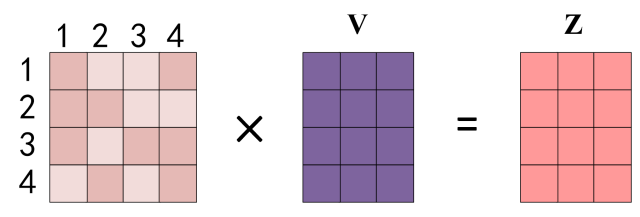
怎么理解呢?其实就是对V的各行做一个加权,然后重新覆盖到V的位置上去。
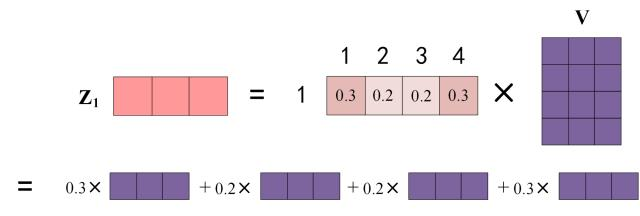
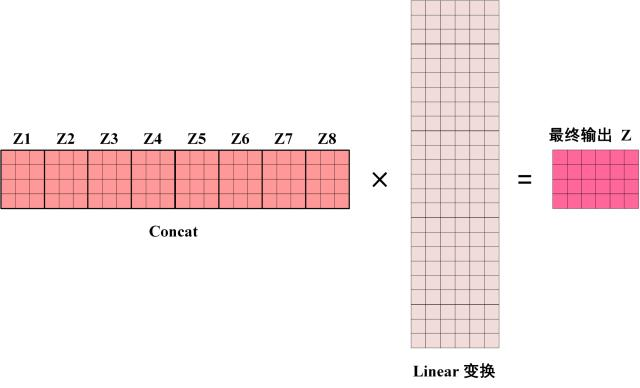
通过这样的操作,就可以得到1头的Z,形状为$(None,max_seq_len,64)$。类似地生成8个头,在最后一维上拼一起,可以得到$(None,max_seq_len,512)$的矩阵。最后再过一个Linear,重新压缩回64维,得到$(None,max_seq_len,64)$的Z。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
class MultiHeadAttention(nn.Module):
def __init__(self):
'''
input_Q: [batch_size, len_q, d_model]
input_K: [batch_size, len_k, d_model]
input_V: [batch_size, len_v(=len_k), d_model]
attn_mask: [batch_size, seq_len, seq_len]
这里并没有按上面的思路写,实际上还是生成了(None,max_seq_len,512)的Q,K,V矩阵,下文通过多创造一个head维,又把512切成8个64维
'''
super(MultiHeadAttention, self).__init__()
self.W_Q = nn.Linear(d_model, d_q * n_heads, bias=False)
self.W_K = nn.Linear(d_model, d_k * n_heads, bias=False)
self.W_V = nn.Linear(d_model, d_v * n_heads, bias=False)
self.fc = nn.Linear(n_heads * d_v, d_model, bias=False)#最终输出还是d_model维的
def forward(self, input_Q, input_K, input_V,mask = False,attn_mask):
'''
X分别过三个线性层,得到Q,K,V,并多加一个n_heads维
这里把X拆成三个输入变量,是为Decoder做准备
'''
residual, batch_size = input_Q, input_Q.size(0)
#终于变成(None,n_head,max_seq_len,64)的矩阵了
Q = self.W_Q(X).view(batch_size, n_heads, max_seq_len,d_q)
K = self.W_K(X).view(batch_size, n_heads, max_seq_len,d_k)
V = self.W_V(X).view(batch_size, n_heads, max_seq_len,d_v)
#attn_mask是一个
attn_mask = attn_mask.unsqueeze(1).repeat(1, n_heads, 1, 1)#构造mask位置的矩阵,传到下面做mask用
context_vector, scores_softmax = ScaledDotProductAttention()(Q, K, V, attn_mask)
output = self.fc(context) # [batch_size, len_q, d_model]
return nn.LayerNorm(d_model)(output + residual), scores_softmax
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
#使用Q,K,V和mask获得词向量的attention版本
class ScaledDotProductAttention(nn.Module):
def __init__(self):
super(ScaledDotProductAttention, self).__init__()
def forward(self, Q, K, V, attn_mask):
'''
Q: [batch_size, n_heads, len_q, d_k]
K: [batch_size, n_heads, len_k, d_k]
V: [batch_size, n_heads, len_v(=len_k), d_v]
attn_mask: [batch_size, n_heads, seq_len, seq_len]
'''
scores = torch.matmul(Q, K.transpose(-1, -2)) / np.sqrt(d_k) # scores : [batch_size, n_heads, len_q, len_k]
scores.masked_fill_(attn_mask, -1e9)#用此函数,在scores的attn_mask处填0,这样避免了矩阵乘法运算
scores_softmax = nn.Softmax(dim=-1)(scores)
context_vector = torch.matmul(scores_softmax, V) # [batch_size, n_heads, len_q, d_v]
context_vector = context_vector.transpose(1, 2).reshape(batch_size, len_q, n_heads * d_v)#转3D,把多头维去掉
return contcontext_vector,scores_softmax#不知道softmax得分有啥呀用处
这个多头注意力层为Decoder部分也留出了操作空间,因为forward里可以传三个独立的输入来生成Q,K,V,同时也能传不同的mask矩阵。
Add&Norm
add&norm接在某个层的后面,指把该层的输入该层的输出相加,也就是所谓的残差链接,可以让网络多关注当前差异的部分,然后把输入的均值方差变成一样的即可。其实使用nn.LayerNorm即可完成Norm,至于Add,自己加就完事了。
Feed Forward
两次Linear层全连接,第一次用了ReLU激活,第二次不激活。论文里在第一层先把维度放大到2048,然后再缩回去。
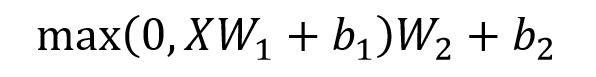
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
class FeedForward(nn.Module):
def __init__(self):
super().__init__()
self.fc = nn.Sequential(
nn.Linear(d_model, d_ff, bias=True),
nn.ReLU(),
nn.Linear(d_ff, d_model, bias=True)
)
def forward(self, X):
'''
X: [batch_size, seq_len, d_model]
'''
residual = X#先保留一份输入
output = self.fc(X)#FF层输出
return nn.LayerNorm(d_model)(output + residual) # [batch_size, seq_len, d_model]
Decoder
从Encoder部分拿到$(None,max_seq_len,64)$形状的矩阵,要做这样一些事情。
1. Multi-Head Attention(带Mask) 2. add&norm 3. Multi-Head Attention 4. add&norm 5. FNN 6. add&norm 7. 然后把它打包重复接六次即可。这里Mask版本的注意力机制在上文已经提到过了,但是第二层注意力略有区别,不是用单输入一口气产出Q,K,V三个矩阵。相反,我们根据 Encoder 的输出 enc_outputs计算得到 K, V,根据上一个 Decoder block 的输出 Z 计算 Q(第一层用输入矩阵decoder_inputs计算Q)。显然,这样计算蕴含了全部的单词信息。
结果输入
得到decoder_outputs后,还要接一个Linear,一个softmax激活,就能得到最终的输出啦!
未完待续……(代码未补全)